About

This project is a collaboration between Felipe Cucker & Hector Rodriguez.

The methodology used in the work involves the choice of a set of fixed dictionaries or databases of images. Each dictionary has its own distinctive quality. For instance, some consist of linear or curved elements generated procedurally.

Other dictionaries might consist of more complicated images, such as frames from movies or Chinese characters.

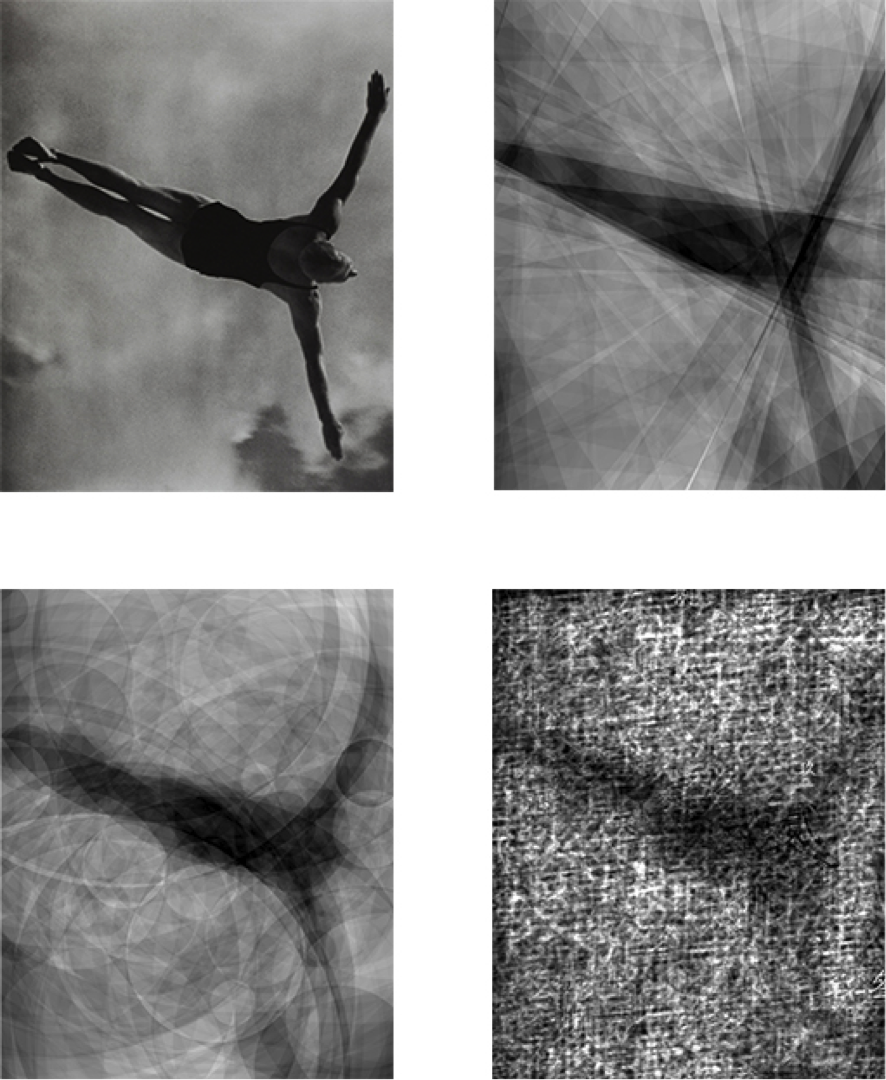
Any other image can then be reconstructed as a weighted superposition of all or some of the images in the dictionary. This set of images is called a basis. For instance, this source image from the 1936 Summer Olympics can be reconstructed by superposing images from a basis of 3840 elements (each of them of the "linear" dictionary).

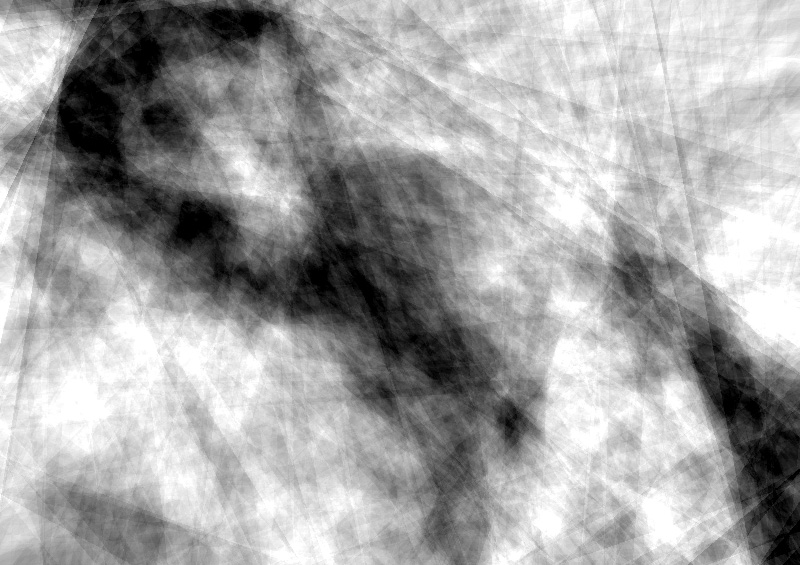
There exist mathematical procedures that identify how to superpose a given subset of images from the dictionary in a manner that most closely reconstructs or "approximates" the source image.

The character of the approximation depends on two kinds of factors: qualitative and quantitative.

The quantitative aspect has to do with the number of images that are used in the reconstruction; i.e., the size of the basis. The sequence of digital prints in Figure 5 shows several reconstructions of one source image using progressively larger bases from the same dictionary.

The qualitative aspect has to do with the character of the images in the dictionary, for instance whether they are linear or curved. Figure 6 shows an image and three reconstructions obtained using bases of the same size from the three dictionaries shown in Figures 1-3. While the three results resemble the original, each has its own distinctive personality.

This video illustrates the qualitative aspect of approximation theory. It shows reconstructions of short clips done with the three dictionaries above. In all three cases the size of the basis is moderate (250 images). This allows the viewer to focus on the reconstruction of the motion rather than on the accuracy of detail.

Our work uses source images drawn from the 1936 Summer Olympics, as shot by director Leni Riefenstahl. These images express a fascination with the human form, and one of our main concerns has to to do with the representation of the body in an algorithmic age. The images are also drawn from an age where the threat of fascism was very real, and manifested itself in the cult of the body. We are also confronting a growing sense of populist authoritarianism around the world. Our response to this threat is to reassert the value of rational analysis and the integration of art, science, and cultural critique. An additional reason to choose Riefenstahl's movie is that it naturally provides a diverse, yet thematically coherent, collection of short clips, rich in movement. The reconstruction of these clips with different dictionaries allows for a visual comparison of the dictionaries' characters.

This project can be exhibited as a set of prints that explore different aspects (both qualitative and quantitative) of mathematical approximation theory, together with videos that compare different reconstructions. The number of prints and videos can be adjusted to take into account venue and equipment constraints.

One of the strengths of this project is the close connection between art, mathematics, and philosophy.

The philosophical aspects have to do with aesthetics. Philosopher Richard Wollheim claims that the experience of seeing a representational image, such as a painting, requires or invites a “twofoldness of attention”^(1)(2)(3)(4). The viewer must attend to:

1. The design properties of the physical medium or support (configurational fold), and
2. The scene or content represented (recognitional fold) by means of those properties.

These two folds are aspects of a single experience, which characterizes representational painting. We see the design properties as responsible for the appearance of the scene depicted. In other words, the recognitional fold is experienced as dependent on the configurational fold.

In some works of visual art, however, attention is devoted mainly to the scene rather than to the manner in which the scene is depicted. The recognitional fold then gains primacy over the configurational fold. For example, the ideal of perspective painting as a transparent window onto the world expresses the primacy of the recognitional over the configurational. In its most extreme version, for instance in photorealist painting, the medium becomes transparent and we see the scene through it. Other artists, however, emphasize the role of the medium. Impressionist and cubist painting can be viewed in this light. Chinese ink painting also highlights the configurational properties of the medium. In this case, we see the scene in, rather than through, the medium.

This distinction between seeing-through and seeing-in provides an important motivation for Approximation Theory.

The quantitative aspects of approximation determine the relationship between the configurational and recognitional folds in the reconstruction of an image. As the size of the chosen basis increases, the image becomes more and more immediately recognizable. The element of seeing-through eventually takes over and we perceive the scene rather than the medium. If the size of the basis becomes very large, then the qualitative character of the dictionary becomes irrelevant and all reconstructions tend to look alike, regardless of the dictionary used.

If the basis is very small, the content is not recognizable, and one can hardly speak of a representational image at all. But if the basis is neither too small nor too large, we see both the medium (the qualitative character of the images in the dictionary) and the content (the image being reconstructed). More crucially, we see the medium as responsible for our seeing the content. We see the content in the medium.

The mathematical concept of the work is in this sense intimately connected to a philosophical reflection on the nature of artistic representation.

 

 

_____________