About

Theorem 8.1 is a 3-channel video projection installation exploring the intersection of art and mathematics. It investigates the artistic possibilities of the mathematical concept of orthogonal projection.

Given a set of digital images (the "dictionary"), orthogonal projection decomposes any source image into a weighted sum of those dictionary images. The elements of the dictionary are brightened or darkened by definite amounts so that their mixture approximates as closely as possible the source image.

Orthogonal projection is used in many practical digital signal processing applications, for instance to extract information from incomplete data or to reduce the complexity of high-dimensional data. The aim of this project is to open up this technological black box, to foreground the computational process involved, and to experiment with its artistic possibilities. The mathematical concept is investigated not as a practical tool but as an end in itself.

A fixed dictionary of still images from the film Alphaville (Jean-Luc Godard, 1965) is first selected. Then four disjoint sets of 30 images are extracted from this dictionary. Every image in the movie is then orthogonally projected onto each of the four sets of frames.

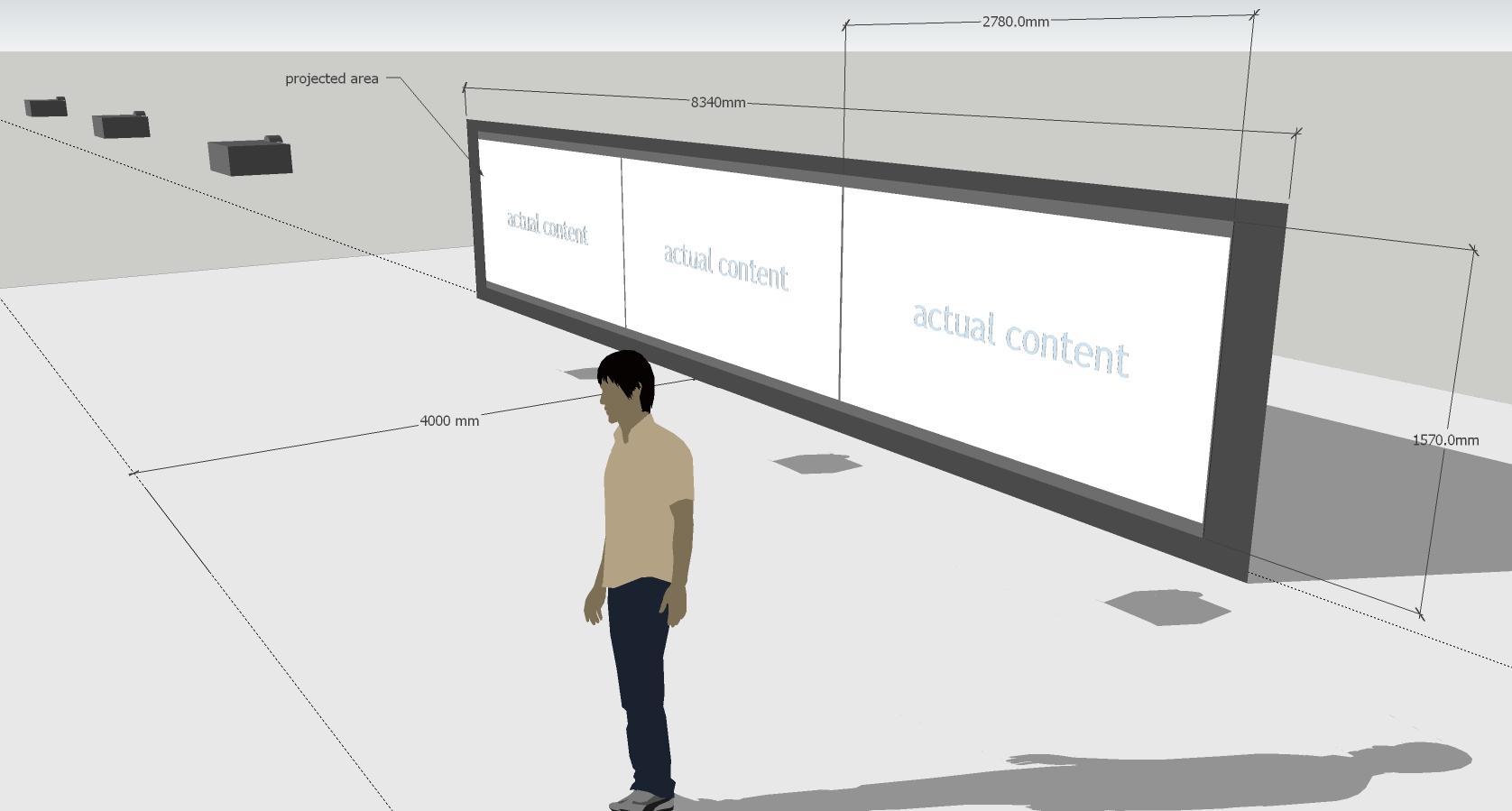
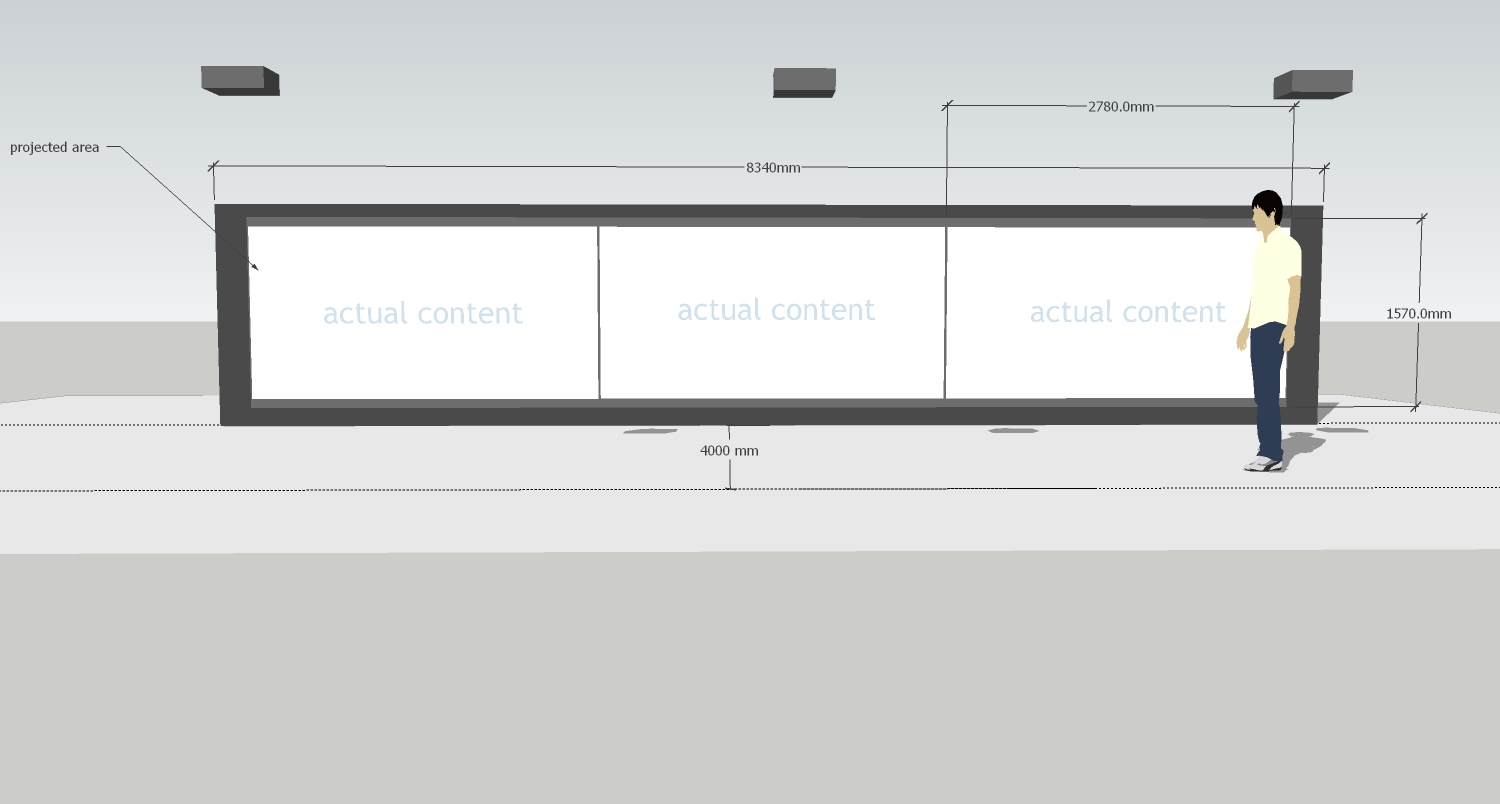
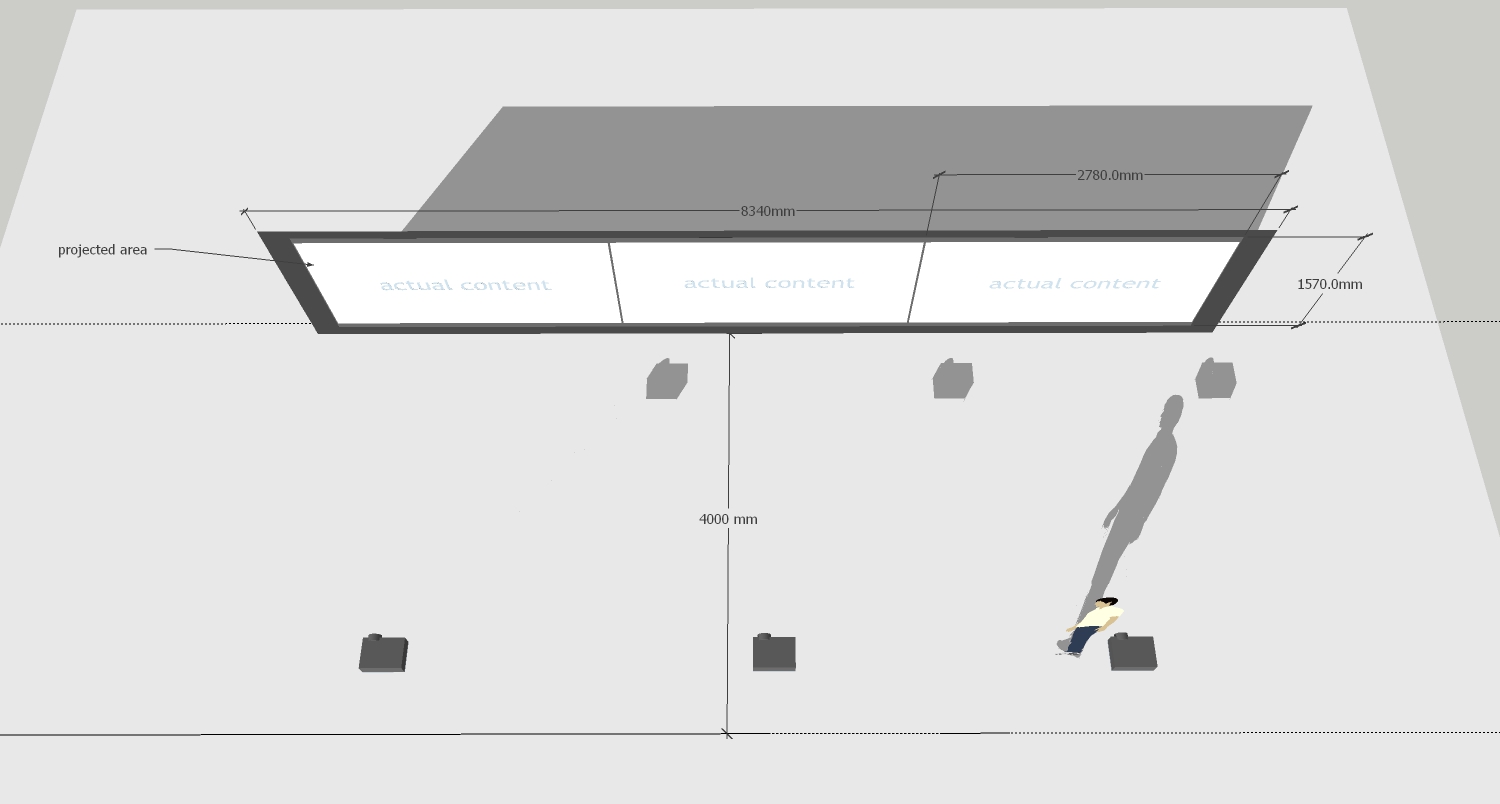
The installation consists of three video projection channels. In the center channel, the full original movie is shown in chronological order together with the four reconstructions.

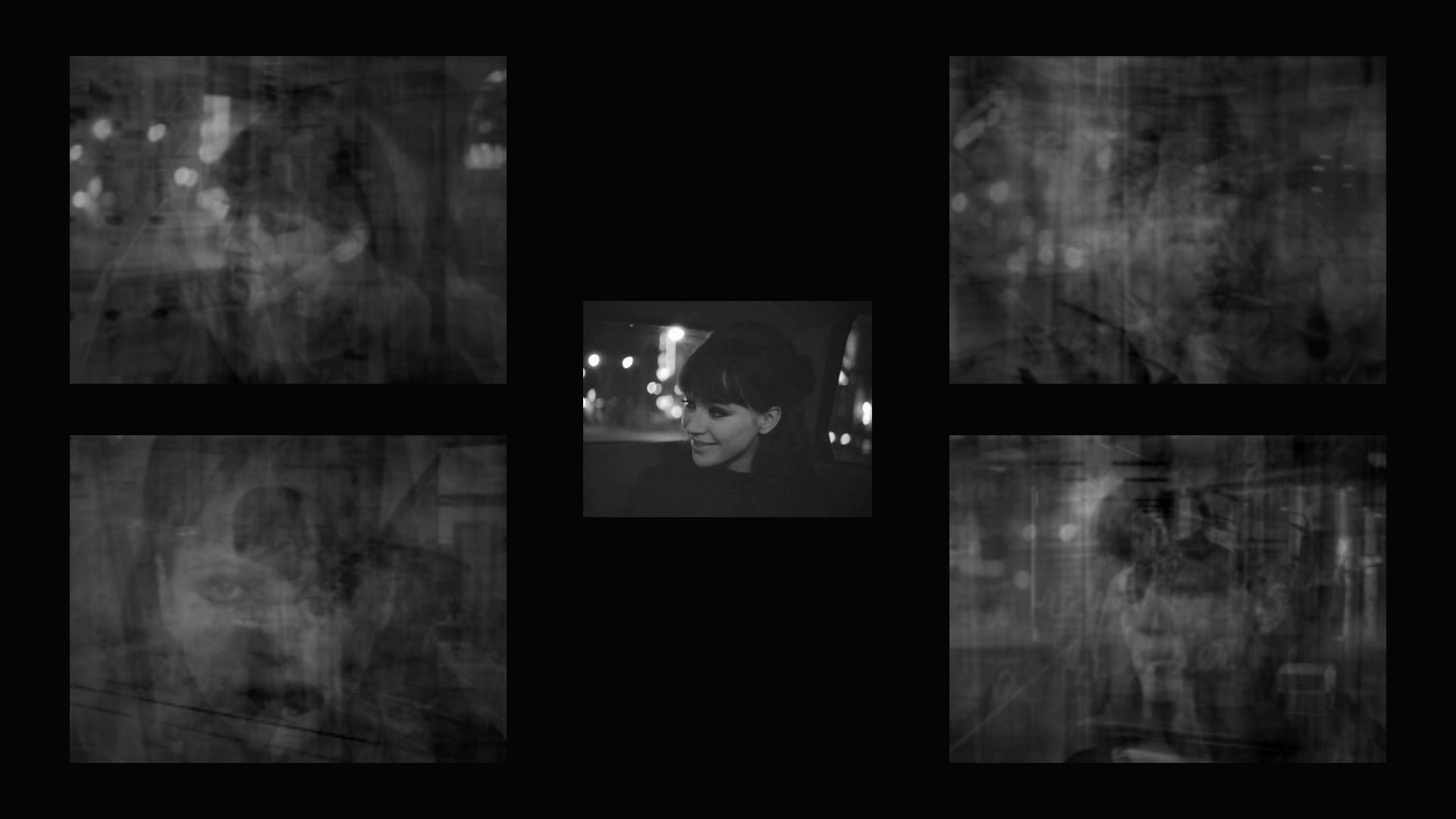
The left and right panels show the four sets of frames used in each the four decompositions.

The three channels are to be projected onto one single wall.

A detailed technical description, which explains the procedure employed in detail, is available here.

A video documentation describing and documenting the project can be found here .

Philosophical and social context of the work

Theorem 8.1 has been developed with social and cultural concerns in mind. The French philosopher Bernard Stiegler has noted that one of the most prevalent processes in contemporary culture is a widespread destruction of knowing-how. (Stiegler, 2010, p. 30.) According to Stiegler's analysis, every technical innovation makes possible an externalization of knowledge. For instance, the techniques of writing make possible an externalization of memory onto (e.g.) physical paper. Memory is materialized in some physical medium. In the process of externalizing ourselves, we also change ourselves. (Stiegler, 2015, p. 107.) There is a harmful aspect to these changes. As we come to rely more and more on technological exteriorizations, such as for instance computational media, artists lose more and more knowledge. (Stieger, 2015, p. 127.) In particular, we no longer know how to do things. For instance, a graphic designer can emboss a digital image using a software package like Photoshop with a click of the mouse. It is only slightly more difficult to assemble ("stitch") a set of photographs into large panoramas. New technologies appear to augment our capacities for doing things, but the supposedly competent user does not need to understand the algorithms that work behind the scenes to make these outcomes possible. As a result, the artist who uses the software is under the illusion that s/he knows how to emboss images or how to create panoramic images, but in fact has no conception of what these procedures actually involve. The artist dissociates her/himself from the mathematical foundation of her/his own tools, which become black boxes. This ignorance masquerading as knowledge prevails in the modern world. Stiegler describes this destruction of knowledge as a process of de- skilling whose outcome is "systematic stupidity" (Stiegler, 2010, p. 45.) We believe that Stiegler's diagnosis accurately and persuasively captures a crucially important aspect of our contemporary predicament as citizens and artists.

What can artists do to address this situation? One possible direction involves a practice of experimental exploration at the intersection of art and computational mathematics. This practice must satisfy two constraints. First of all, the artist must open at least one technological black box. The artist, often in collaboration with a scientist, chooses one or more computational technologies and acquires at least a basic theoretical knowledge and practical knowledge (knowing-how) of those technologies. The artist thus refuses to use technologies without actually understanding them. Instead of rejecting technology, the artist engages critically and reflectively with it. By proceeding in this way, the artist works to overcome the stupidity that Stiegler diagnoses. In Theorem 8, for instance, the artist chose to explore the concept of orthogonal projection, an idea that has been applied, for instance, in compute vision algorithms.

Secondly, the artist must not use this technology for some instrumental purpose, such as surveillance, face recognition, or image compression. Rather, the artist must investigate possible ways of connecting the abstract mathematical concepts that undergird this technology to concrete visual (or otherwise perceptible) experiences and diverse subject positionings. This critical investigation becomes an end in itself. The artist does not aim to achieve a practical end but rather to explore the intrinsic possibilities and limitations of the technology and its relation to the field of the visible. Possibly in collaboration with a scientist, the artist develops a research direction based on definite and systematic questions that arise in part from a mathematical or scientific framework. The questions take the following general form: What are the possible ways of relating the mathematical concepts that undergird this technology with perceptual experiences, and what are the tensions or limitations of these relations? These questions must orient her/his experimental art practice.

_____________

Preferred Setup

The preferred setup consists of 3 ceiling-mounted full HD (1920 x 1080) projectors and a white wall. The actual video consists of 3 screens, with each screen having a 16:9 aspect ratio (depicted in white). The 3 screens should be of the same size with no space in between. The work should be shown in a completely dark environment.

hardware requirements

- PC with PCI graphic card // best resolution: 3 x ( 1920 x 1080 ) // min resolution: 3 x ( 1280 x 720 )
- matrox TripleHead2Go monitor splitter // min model: digital edition, 3 x ( 1920 x 1080 )
- 3 x projectors, ceiling mounted // best resolution: 1920 x 1080 // min resolution: 1280 x 720

software requirements

- vlc player for video playback ( video format: *.mp4 or *.mov, h.264, 5760x1080 )

Simple Setup

Theorem 8.1 can also be exhibited using display monitors in place of projectors, which can be shown using three frameless 16:9 monitors (of the same model) aligning side by side. The monitors should have a minimum of 42in (107cm) diagonal.

Mathematical framework

This page contains a comprehensive description of the algorithm employed in Theorem 8.1. It is intended for the mathematically literate reader who wishes to acquire a more precise and in-depth understanding of Theorem 8.1. A certain background in elementary linear algebra is presupposed.

1. The Algorithm

A grayscale image of n pixels can be considered as a vector in ℝⁿ. Any set of k linearly independent images ("the dictionary") determines a k-dimensional subspace of ℝⁿ. Any vector v in ℝⁿ can be approximated as a linear combination of images in the dictionary by the following method:

Let A_{n x k} be a matrix consisting of the k images in the dictionary. The ( i, j )^th entry of A contains the i-th pixel of the j-th image. To project a given vector v in ℝⁿ onto the subspace spanned by A, we need to obtain the vector c of coefficients

c = A⁺ v

where A⁺ denotes the Moore-Penrose pseudo-inverse of A, or

A⁺ = (A^T A)^-1 A^T

We wish to reconstruct the input vector v as a weighted sum of images in A. The coefficients in c express the contributions of the individual dictionary images to the reconstruction. The first coefficient represents the weight of the first image in the dictionary, and so on. The sign (positive or negative) of each coefficient specifies whether that image is to be added to or subtracted from the other images in the dictionary.

Given the coefficients, the orthogonal projection p of v onto the subspace spanned by the vectors is

p = A c

The entire algorithm can be concisely expressed in one line as:

p = A (A^T A)^-1 A^T v

The source for the class that computes the orthogonal projection of a vector is available here.

2. Visualization challenges

The principal aim of Theorem 8.1 is to make visible the computational process that underpins the concept of orthogonal projection. To paraphrase Gregory Bateson's well-known definition of information, we may say that the visualization method has been designed to render visible every "difference that makes a difference" to the underlying computation. With this goal in mind, the exhibition display shows the changing coefficients of each image in a subset of the dictionary and the resulting approximate reconstruction of each source frame in the running movie.

The algorithm used to compute the orthogonal projection of an image does not assume that the columns of the dictionary matrix A are orthonormal or even orthogonal. This approach is one of the distinguishing marks of Theorem 8.1 relative to the earlier version of this project, Theorem 8. In the previous version, the images in the dictionary were first pre-processed using the Gram-Schmidt procedure, to ensure that they were orthonormal. This approach facilitated certain computations, but it resulted in a dictionary with vectors containing both positive and negative brightness values. Negative pixel values could not be translated directly into physical light intensities and were set to zero for the purposes of visualization. A consequence of this decision was a considerable loss of data in the final visual display. In contrast, the current version does not pre-process any of the frames in the dictionary. Pixel values are always represented as numbers in the range [0, 1], with 0 denoting a black pixel and 1 denoting a white one. There are no dictionary elements with negative pixel values.

The goal of aesthetic visualization poses another challenge. The orthogonal projection of a given v onto the subspace spanned by A sometimes outputs a linear combination with negative coefficients. Let c_j be a negative coefficient corresponding to dictionary image A_j. How is product of this negative coefficient with the values in A_j to be visualized? The solution adopted here (suggested by Felipe Cucker) is the following: If c_j < 0, every brightness value A_i,j is replaced with (1 - A_i,j ) and then multiplied by the absolute value of c_j. This transformation replaces the dictionary element with its "negative" image (where the word "negative" has its usual photographic meaning).

This solution contrasts with the approach adopted in Theorem 8. In that case, the use of the Gram-Schmidt procedure as a pre-processing step meant that every frame in the dictionary had some positive and negative pixels. Multiplying any frame by a negative coefficient transformed negative pixel values into positive ones and vice versa. For visualization purposes, negative pixel values were set to zero (black), which resulted in a considerable loss of information. In this new version, the images in the dictionary are not preprocessed; since all pixel values are positive, the multiplication of any dictionary image by a negative coefficient would turn all of its pixels into negative values. Adopting the same solution as in Theorem 8 would in such a case produce a completely black image. The alternative solution adopted here preserves more information and so gives a more comprehensive picture of the underlying computation (although the approach employed in Theorem 8 has its own distinctive visual character).

The connection between the mathematical and artistic aspects of the work lies here: every aesthetic decision has been made with an eye to rendering perceptible every difference that makes a difference to the computation of the orthogonal projection of an image.

3. Selection of frames in the dictionary

In Theorem 8.1, the dictionary consists of frames extracted from Godard's Alphaville. Every image in the film is then projected onto a subset of this dictionary.

How were the frames in the dictionary selected? Frames from Godard's Alphaville were chosen by a sequential method. The magnitudes of every frame f in the frequency domain (after a Discrete Fourier Transform) were compared with those of r immediately preceding frames. Image f was selected for inclusion in the dictionary if the difference was higher than a fixed threshold.