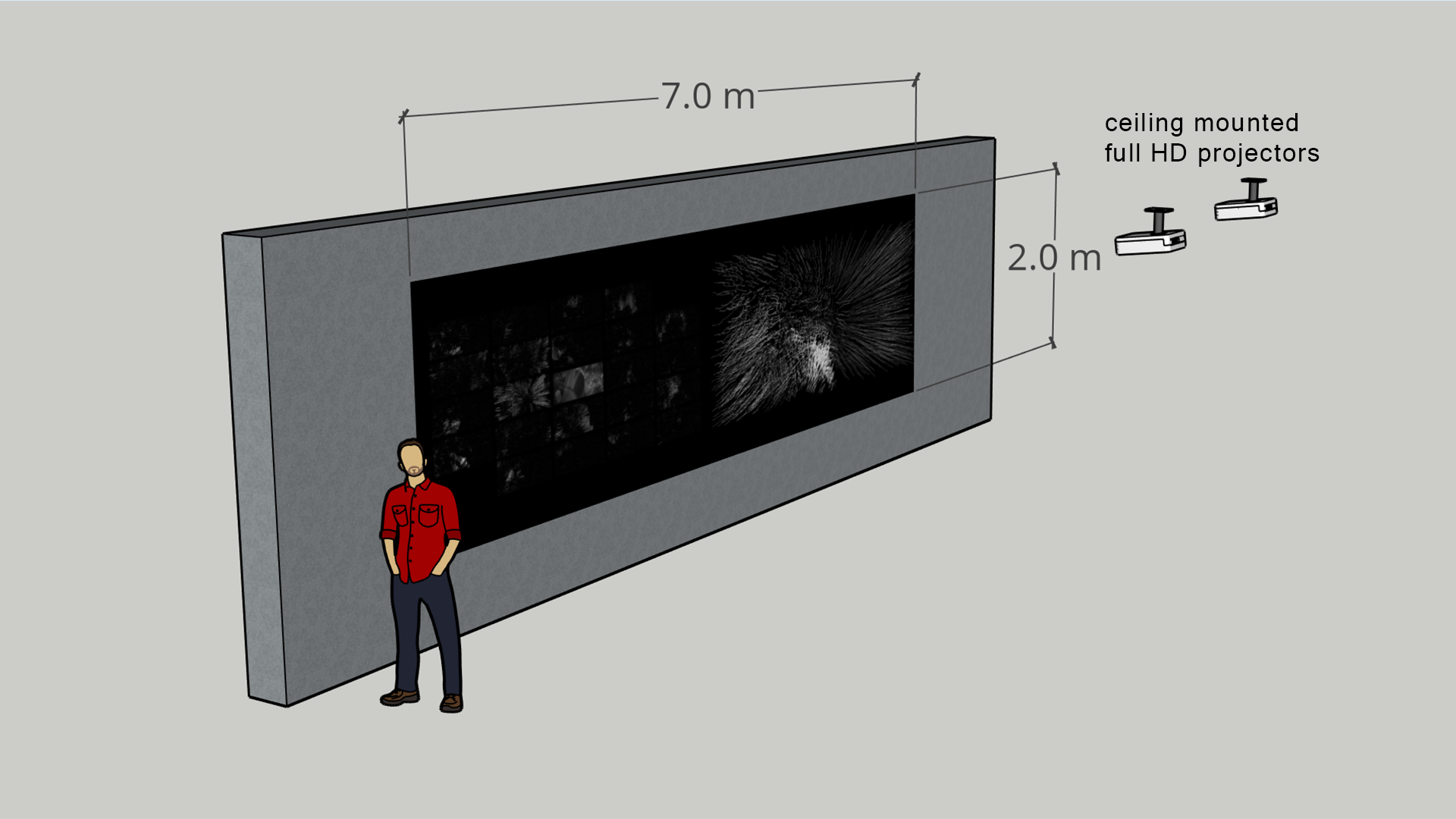
OVERVIEW
Errant version 2: The Kinetic Propensity of Images is a project about the automatic analysis and visualization of motion in the cinema. A newly designed machine learning algorithm decomposes the movement in every sequence of a movie into a set of elementary motions. These elementary motions are then recombined to produce a reconstruction of the visible movement in the sequence. The analysis and reconstruction are displayed as a two-channel video installation. The visualization of the movement uses a variant of the streakline method often employed in fluid dynamics.
The following image is an instance of the left channel. The original movie frame is shown together with eight motion factors discovered by the algorithm.

The following image is an instance of the right channel for the same frame. The movement at that instant is reconstructed by combining the eight motion factors.

The algorithm for this work has been completely redesigned from the original version of this project. That version produced a dictionary that contains many different factors. These factors were often redundant and sometimes very difficult to interpret. Version 2.0 uses a different approach for both data representation and data factorization that produces a smaller and more interpretable dictionary. The original algorithm produced a different dictionary for every shot. Algorithm 2.0 learns one single dictionary for the entire film, so that viewers can more easily compare and contrast the activation patterns of different sequences. Details are in the algorithm section of this website.
The movie being analyzed is Ugetsu Monogatari (Mizoguchi Kenji, 1953). This cinematic text was selected mainly for its carefully choreographed long takes. But there is a sociopolitical subtext to the choice of both film and machine learning methodology.
The machine learning algorithms used to analyze and synthesize motion are all specifically designed for this work, but they are variants of methods primarily used for the purpose of crowd control and abnormal movement detection. This project is a “detournement” of surveillance techniques to analyze and foreground movements in movies that attack authoritarianism. More specifically, the film chosen was made by Mizoguchi as a response to the Second World War, and more specifically, to a situation where people were dominated by their own fascistic and militaristic governments. The motions in the film are closely related to this situation.
The original version of this work was commissioned by Linda Lai for the exhibition Algorithmic Art: Shuffling Space and Time, held at the Hong Kong City Hall, December 27 2018 - January 10 2019. Production was partly funded with a grant from the Innovation Technology Fund of the Hong Kong government. Production of the new version was funded by a fellowship from the Centre for Advanced Computing and Interactive Media (ACIM) of the School of Creative Media of the City University of Hong Kong. The project was made at the Perceptron Lab founded by Héctor Rodríguez.